Se denomina movimiento rectilíneo, cuando su trayectoria es una línea recta. En la recta situamos un origen O, donde estará situado un observador, que medirá la posición del móvil x en el instante t. Las posiciones serán positivas si el móvil está a la derecha del origen y negativas si está a la izquierda del origen. La posición x del móvil se puede relacionar con el tiempo t mediante una función x=f(t). Desplazamiento Supongamos ahora que en el tiempo t, el móvil se encuentra en posición x, más tarde, en el instante t' el móvil se encontrará en la posición x'. Decimos que móvil se ha desplazado Dx=x'-x en el intervalo de tiempo Dt=t'-t, que va desde el instante t al instante t'. La velocidad media entre los instantes t y t' está definida por Para determinar la velocidad en el instante t, debemos hacer el intervalo de tiempo Dt tan pequeño como sea posible, en el límite cuando Dt tiende a cero. Pero dicho límite es la definición de derivada de x con respecto del tiempo t. En general, la velocidad de un cuerpo es una función del tiempo. Supongamos que en un instante t la velocidad del móvil es v, y en el instante t' la velocidad del móvil es v'. Se denomina aceleración media entre los instantes t y t' al cociente entre el cambio de velocidad Dv=v'-v y el intervalo de tiempo en el que se ha tardado en efectuar dicho cambio, Dt=t'-t. La aceleración en el instante t es el límite de la aceleración media cuando el intervalo Dt tiende a cero, que no es otra cosa que la definición de la derivada de v. Si conocemos un registro de la velocidad podemos calcular el desplazamiento x-x0 del móvil entre los instantes t0 y t, mediante la integral definida. El producto v dt representa el desplazamiento del móvil entre los instantes t y t+dt, o en el intervalo dt. El desplazamiento total es la suma de los infinitos desplazamientos infinitesimales entre los instantes t0 y t. En la figura, se muestra una gráfica de la velocidad en función del tiempo, el área en color azul mide el desplazamiento total del móvil entre los instantes t0 y t, el segmento en color azul marcado en la trayectoria recta. Hallamos la posición x del móvil en el instante t, sumando la posición inicial x0 al desplazamiento, calculado mediante la medida del área bajo la curva v-t o mediante cálculo de la integral definida en la fórmula anterior. Del mismo modo que hemos calculado el desplazamiento del móvil entre los instantes t0 y t, a partir de un registro de la velocidad v en función del tiempo t, podemos calcular el cambio de velocidad v-v0 que experimenta el móvil entre dichos instantes, a partir de un registro de la aceleración en función del tiempo. En la figura, el cambio de velocidad v-v0 es el área bajo la curva a-t, o el valor numérico de la integral definida en la fórmula anterior. Conociendo el cambio de velocidad v-v0, y el valor inicial v0 en el instante t0, podemos calcular la velocidad v en el instante t. Resumiendo, las fórmulas empleadas para resolver problemas de movimiento rectilíneo son Un movimiento rectilíneo uniforme es aquél cuya velocidad es constante, por tanto, la aceleración es cero. La posición x del móvil en el instante t lo podemos calcular integrando o gráficamente, en la representación de v en función de t. Habitualmente, el instante inicial t0 se toma como cero, por lo que las ecuaciones del movimiento uniforme resultan Un movimiento uniformemente acelerado es aquél cuya aceleración es constante. Dada la aceleración podemos obtener el cambio de velocidad v-v0 entre los instantes t0 y t, mediante integración, o gráficamente. Dada la velocidad en función del tiempo, obtenemos el desplazamiento x-x0 del móvil entre los instantes t0 y t, gráficamente (área de un rectángulo + área de un triángulo), o integrando Habitualmente, el instante inicial t0 se toma como cero, quedando las fórmulas del movimiento rectilíneo uniformemente acelerado más simplificadas. La primera crítica a la Teoría de la Relatividad Especial (RE) de Einstein en materia de movimiento rectilíneo uniformesistemas de referencia inerciales y no inerciales empleada y empeoran cuando se intenta examinar el fondo. (MRU) es que la terminología de sistemas de referencia inerciales y no inerciales no me gusta por varias razones. La principal es que no estoy a gusto con tantas connotaciones técnicas del concepto, serán limitaciones mías. A continuación expongo unas cuantas ideas que espero justifiquen por qué los problemas empiezan con la terminología de Al mencionar que en los sistemas de referencia inerciales la masa no varía con la velocidad, puede parecer que los sistemas inerciales se corresponden con la mecánica clásica de Newton y los no inerciales con la RE de Albert Einstein, pero no tiene nada que ver; la Relatividad Especial versa sobre los sistemas de referencia inerciales y la Relatividad General (RG) sobre los no inerciales. Tampoco se corresponden con la idea de movimiento relativo entre sistemas con movimiento rectilíneo uniforme o MRU. En ocasiones se dice que el principio de relatividad de Galileo permite asegurar que todos los sistemas de referencia inerciales son equivalentes y que se puede pasar de uno a otro sin alterar las variables de tiempo, masa, aceleración y fuerza. Sin embargo, no parece muy correcta la anterior afirmación, un sistema de referencia inercial que esté en movimiento rectilíneo uniforme (MRU) respecto a otro sistema de referencia no daría las mismas medidas de la masa por tener una velocidad diferente, tampoco la fuerza necesaria para acelerar la distinta masa sería igual, etc. Se podría argumentar que lo que ocurre es que para velocidades pequeñas las diferencias mencionadas serán despreciables; pero conceptualmente sigue siendo erróneo. Es más, todos los sistemas de referencia son no inerciales, incluso aquéllos que están en movimiento rectilíneo uniforme entre sí, aunque para ciertos análisis parciales o estudios concretos se pueda suponer que son inerciales. Es algo similar a lo que ocurre con el concepto de vacío, el vacío propiamente dicho no existe, siempre hay gravedad. Asimismo, hay que reconocer que hablar de la aparición de fuerzas ficticias en los sistemas de referencia no inerciales le da un toque melodramático a esta materia, y algunas neuronas empiezan a pensar en cuándo acabará la pesadilla donde se han metido y qué han hecho para merecer eso. Por otra parte, se habla de sistemas inerciales y no inerciales y no se emplea lo de sistemas acelerados o no aceleradosprincipio de equivalencia entre gravedad y aceleración de la relatividad general. porque hay sistemas que no están en movimiento pero se consideran equiparados a los acelerados por el Es decir, en el nombre de un concepto básico se están incluyendo múltiples conceptos y algunos bastante avanzados. Puede ser útil para los especialistas (aunque no se nota) pero para los que intentan comprender la relatividad sin dedicarle cincuenta años supone un contratiempo importante. Más que una ciencia que simplifique la realidad física parece... me recuerda el lenguaje... y toda su riqueza geográfica. Es más, el término inercial me suena a la inercia de las cosas a seguir en su trayectoria, bien sea física, histórica o de cualquier otra circunstancia. Pero un sistema acelerado también implica inercia aunque ésta no sea la única causa de su movimiento. ¡Quizás los sistemas no inerciales se deberían llamar sistemas súper-inerciales! Así, resulta que un concepto que se utiliza para delimitar el ámbito teórico de la Relatividad Especial de Einstein es contrario a su sentido más normal en física y además incorpora la noción del principio de equivalencia de la Relatividad General también de Einstein. También conviene tener en cuenta que cuando se habla de sistemas inerciales o no inerciales se debería estar hablando de la relación entre dos sistemas puesto que todos los sistemas individualmente considerados siempre están en reposo por pura convención de sistema de referencia, salvo, volvemos a lo anterior, que estemos hablando de un sistema en un espacio con gravedad. La estructura reticular de la gravedad o globina y el significado físico de la equivalencia masa energía se expone en el libro en línea de la Mecánica Global, dentro de la nueva teoría de todo de la Teoría de la Equivalencia Global. Las implicaciones de la gravedad sobre el concepto de movimiento, fuerza y el mecanismo reticular de la energía cinética de la pulsina se estudian en profundidad en el libro en línea de la Dinámica Global. Volviendo a tema, ¡En un sistema de referencia inercial puede haber objetos acelerados! Una razón adicional por la que no me gusta la terminología empleada es que también se denominan a los observadores como inerciales o no inerciales. Para ver el efecto sobre el cerebro de toda esta forma de expresarse nos podemos preguntar cómo vería un observador no inercial a un objeto inmóvil en un sistema de referencia inercial. ¡Sencillo! ¿No? Avanzando en la sencillez del modelo, los conceptos de observadores inerciales y observadores no inerciales se utilizan como si la realidad física dependiera de ellos. ¡Ah, pero si se trata de eso! Yo siempre hubiera pensado que se trata de un cambio de punto de vista, de sistema de medidas, de gafas, de lo que sea; pero que la realidad física, si existe, es una. ¡O dos como mucho! Sobre esta dependencia versa y prosa el punto sobre La teoría del observador ignorante del apartado de Física relativista y matemáticas de este libro en línea. Ya voy entendiendo por qué mi padre, cuando yo era pequeñito, hablando de cosas con otros mayores, repetía más de la cuenta la frase: "No se debe confundir la velocidad con el tocino". Lo repetía, no demasiadas veces, pero lo suficiente como para notarse que él pensaba que había demasiadas flexibilidades conceptuales. ¡No me puedo imaginar lo que hubiera dicho si hubiera estudiado Física Moderna! A efectos prácticos, creo que lo que se pretende identificar son modelos donde se prescinde del efecto de los cambios en la masa debidos a la velocidad (por movimiento rectilíneo uniforme o no) o efectos similares debidos a la existencia del campo gravitatorio (sistemas de referencia inerciales) o, por el contrario, se tienen en cuenta (sistemas de referencia no inerciales). Dicho de otra forma, en los sistemas de referencia inerciales el tiempo relativo sólo depende de las diferencias de velocidad de acuerdo con las previsiones de la Relatividad Especial de Einstein mientras que en los sistemas de referencia no inerciales además se producirán efectos indirectos sobre el tiempo explicados por la Relatividad General en base a su principio de equivalencia. No-distinción entre la velocidad física o real y la velocidad relativa, mental o abstracta Veamos un ejemplo sencillo que nos ilustre sobre la idea de la velocidad máxima en la Teoría de la Relatividad de Einstein. Para hacerlo más intuitivo, vamos a suponer que las pelotas que se muestran en la figura son partículas pequeñas que salen disparadas con movimiento rectilíneo uniforme en sentido contrario con una velocidad 0,9 c. Al medir su velocidad relativa obviamente obtendremos 1,8 c puesto que después de un segundo estarán separadas por 5,4 * 108 metros debido a su movimiento rectilíneo uniforme. Por el dogma, axioma o como se quiera llamar (todo menos comprobación experimental) de que c es la velocidad máxima el resultado no puede ser correcto y, efectivamente, aplicando las fórmulas "adecuadas y correctas" nos da que dicha velocidad es 0,994 c, el tiempo es 4,152 segundos en lugar de uno y que el espacio es 12,388 * 108 metros. ¡Digamos, algo así como el mínimo común múltiplo asintótico-pitagórico! Esta es una de las ideas más claras en contra de la Teoría de la Relatividad de Einstein, por eso utilizo un título de la figura especialmente llamativo. Se está imponiendo un límite máximo no ya a la velocidad de la luz o velocidad física sino a una velocidad que sólo existe en la mente, pues la velocidad de separación es claramente un concepto mental. Justo es reconocer que hay división de opinión en los físicos consultados respecto a esta existencia de velocidad 2c o cercana. Parece como si la relatividad también afectase a las opiniones técnicas, me recuerda la defensa India de enroque clásico o la supervivencia por adaptación darwinista. En consecuencia, es absolutamente automática la necesidad de hacer relativo el tiempo y todo lo que se ponga por delante. ¡Por puro diseño del modelo! Se aplica la transformación asintótica de la velocidad relativista para que nunca supere c " ... y todos comieron perdices y fueron felices. Claramente, deben existir razones poderosas para que la comunidad científica acepte esta forma de proceder durante un siglo. Nos pasa a todos con las casualidades, cuando dos cosas muy raras coinciden, normalmente asumiremos que el único factor común que podemos encontrar es el relevante para explicarlas. En el caso de la Teoría de la Relatividad coincidieron bastantes más cosas raras y no es de extrañar que se aceptara en su día. Siguiendo con el tema del ejemplo, estos supuestos de velocidades abstractas más elevadas son totalmente verificables en infinidad de casos. Basta con citar todos los fotones antípodos de todas las estrellas luminosas. Por lo tanto, la dilatación del tiempo y contracción del espacio que se propone es totalmente artificial e imaginaria. Me surge otra duda, si la velocidad máxima de la luz es *c*, ¿dónde se encuentra la necesidad de realizar una transformación asintótica para evitar que la supere? Me temo que todos los casos en que se utilizan las transformaciones de Lorentz son en cierto sentido asimilables al de este ejemplo. Por último, se puede hacer la argumentación filosófica de que cuando hacemos una pelota origen de referencia espacial no podemos saber si está en reposo físico o no, ¿qué pelota es la que se mueve? Y, por lo tanto, le aplicamos las fórmulas convencionales donde c es la velocidad máxima. Esta justificación no añade nada nuevo, la ignorancia de las pelotas sobre cuál de ellas está en movimiento (sea en movimiento rectilíneo uniforme o geodésico), no exime que la realidad exista con unas leyes físicas que cumplir y, a ser posible, que tengan un mínimo sentido común.
Un movimiento es rectilíneo cuando describe una trayectoria recta y uniforme cuando su velocidad es constante en el tiempo, es decir, su aceleración es nula. Esto implica que la velocidad media entre dos instantes cualesquiera siempre tendrá el mismo valor. Además la velocidad instantánea y media de este movimiento coincidirán.
La distancia recorrida se calcula multiplicando la velocidad por el tiempo transcurrido. Esta operación también puede ser utilizada si la trayectoria del cuerpo no es rectilínea, pero con la condición de que la velocidad sea constante.
Durante un movimiento rectilíneo uniforme también puede presentarse que la velocidad sea negativa. Por lo tanto el movimiento puede considerarse en dos sentidos, el positivo sería alejándose del punto de partida y el negativo sería regresando al punto de partida.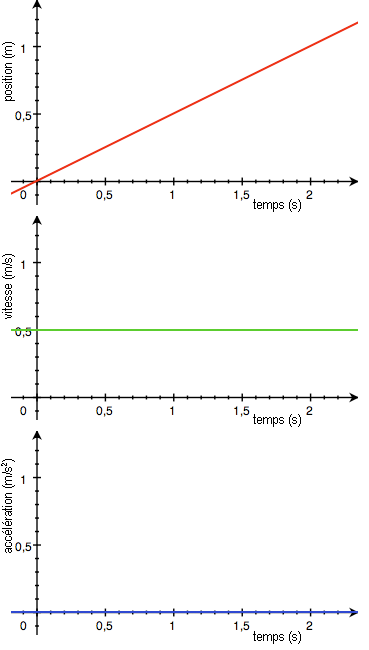
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
Movimiento rectilíneo

Posición

Velocidad
![]()
![]()
Aceleración

![]()
![]()
Dada la velocidad del móvil hallar el desplazamiento


Dada la aceleración del móvil hallar el cambio de velocidad



Movimiento rectilíneo uniforme
![]()


Movimiento rectilíneo uniformemente acelerado
![]()

![]()


II.c.1.b) Movimiento rectilíneo uniforme (MRU) y relatividad
![]()
De acuerdo a la 1ª Ley de Newton toda partícula permanece en reposo o en movimiento rectilíneo uniforme cuando no hay una fuerza neta que actúe sobre el cuerpo.
Esta es una situación ideal, ya que siempre existen fuerzas que tienden a alterar el movimiento de las partículas. El movimiento es inherente que va relacioneado y podemos decir que forma parte de la materia misma.
Ya que en realidad no podemos afirmar que algún objeto se encuentre en reposo total.
El MRU se caracteriza por:
a)Movimiento que se realiza en una sóla direccion en el eje horizontal.
b)Velocidad constante; implica magnitud y dirección inalterables.
c)Las magnitud de la velocidad recibe el nombre de rapidez. Este movimiento no presenta aceleración (aceleración=0).
Relación Matemática del MRU:
El concepto de velocidad es el cambio de posición (desplazamiento) con respecto al tiempo.
Fórmula:
v= d/t ; d=v*t ; t=d/v
v=velocidad d=distancia o desplazamiento t=tiempo
MECÁNICA: Parte de la Física que estudia el movimiento, lo que lo produce y lo que lo modifica y afecta y se divide en:
Ciniemática:Estudia el movimiento sin importar las causas.
Dinámica:Estudia el movimiento así como sus causas.
Dentro del movimiento existe un móvil (el que se mueve) y el camino que sigue éste (trayectoria).
Distancia:Cantidad escalar. Que tanto recorre el móvil.
Desplazamiento:Cantidad vectorial. Es la distancia con su dirección.
Rapidez:Cantidad escalar y es la relación de la longitud con un intervalo de tiempo.
Velocidad:Cantidad vectorial, relación del desplazamiento en un intervalo de tiempo.
Velocidad y Rapidez Instantanea: Medición en el momento en un punto arbitrareo.
Velocidad y Rapidez Media:Promedio entre la velocidad inicial y la velocidad final. (Vi y Vf) Vi+Vf/2.
Velocidad y Rapidez Promedio:Distancia recorrida entre el tiempo transcurrido en recorrer dicha distacia.
PROBLEMA
Un corredor trota de un extremo a otro de la pista en línea recta 300m en 2.5 min., luego se voltea y trota 100m hacia el punto de partida en otro minuto.
1.-¿Cuáles son la rapidez y velocidad promedio del trotador al ir del punto A al B y del punto B al C?
2.-¿Cuál es la rapidez y velocidad media del trotador para los mismos casos?
1.-a) rprom= 300m/2.5min=120 m/min
b)rprom=400m/3.5 min = 114.28 m/min
a)vprom=300m / 2.5 min=120m/min 0º (E)
b) vprom= 200m/3.5min = 57.14 m/min 0º (E)
2.-a) r=ri + rf / 2= 0+120m/min /2 = 60 m/min
b) (0+114.28 m/min /2= 57.14 m/min
a)v= 0+120 m/min /2 = 60 m/min al E
b) v= 0+57.14 m/min /2 = 28.57 m/min al E
3.- rb=120m/min rc= 100m/min
r= 120 m/min+100m/min /2 =
r= 110 m/min.
Rapidez promedio: a)120 m/min b)114.28 m/min
Velocidad promedio: a) 120m/min al E b)57.14m/min al E
Rapidez media: a)60m/min b)57.14m/min
Velocidad media: a)60m/min al E b)28.57m/min al E
GRAFICAS DE MRU.
Al graficar el desplazamiento (distancia) contra tiempo se obtiene ina línea recta. La pendiente de la línea recta representa el valor de la velocidad para dicha partícula.
Al realizar la gráfica de velocidad contra tiempo obtenemos una recta paralela al eje X. Podemos calcular el deslazamiento como el área bajo la línea recta.

0 comentarios