La caída libre como sistema de referencia
Un sistema de referencia ligado a un cuerpo en caída libre puede considerarse inercial o no inercial en función del marco teórico que esté utilizándose.
En la física clásica, la gravedad es una fuerza que aparece sobre una masa y que es proporcional al campo gravitatorio medido en la posición espacial donde se encuentre dicha masa. La constante de proporcionalidad es precisamente el valor de la masa inercial del cuerpo, tal y como establece el principio de equivalencia. En la física relativista, la gravedad es el efecto que produce sobre las trayectorias de los cuerpos la curvatura del espacio-tiempo; en este caso, la gravedad no es una fuerza, sino una geodésica. Por tanto, desde el punto de vista de la física clásica, un sistema de referencia en caída libre es un sistema acelerado por la fuerza de la gravedad y, como tal, es no inercial. Por el contrario, desde el punto de vista de la física relativista, el mismo sistema de referencia es inercial, pues aunque está acelerado en el espacio, no está acelerado en el espacio-tiempo. La diferencia radica en la propia definición de los conceptos geométricos y cinemáticos, que para un marco teórico y para el otro, son completamente diferentes.
Aceleración en caída libre
En este movimiento se desprecia el rozamiento del cuerpo con el aire, es decir, se estudia en el vacío. El movimiento de la caída libre es un movimiento uniformemente acelerado. La aceleración instantánea debida sólo a la gravedad es independiente de la masa del cuerpo, es decir, si dejamos caer un coche y una pluma, ambos cuerpos tendrán la misma aceleración, que coincide con la aceleración de la gravedad ('g').
Cuando la caída libre tiene lugar en el seno de un fluido como el aire, hay que considerar las fuerzas viscosas que actúan sobre el cuerpo. Aunque técnicamente la caída ya no es libre, desarrollaremos en adelante las ecuaciones incluyendo el término aerodinámico excepto en los casos en los que no proceda (p.e. espacio exterior).
Caída libre en campo aproximadamente constante
Sabemos por la segunda ley de Newton que la suma de fuerzas  es igual al producto entre la masa del cuerpo mas la aceleración del mismo. en caída libre sólo intervienen el peso
es igual al producto entre la masa del cuerpo mas la aceleración del mismo. en caída libre sólo intervienen el peso  , que siempre es vertical, y el rozamiento aerodinámico
, que siempre es vertical, y el rozamiento aerodinámico  que va en la misma dirección aunque en sentido opuesto a la velocidad. La ecuación de movimiento es por tanto:
que va en la misma dirección aunque en sentido opuesto a la velocidad. La ecuación de movimiento es por tanto:
siendo m la masa del cuerpo.
La aceleración de la gravedad se indica con signo negativo, porque tomamos el eje de referencia desde el suelo hacia arriba, los vectores ascendentes los consideraremos positivos y los descendentes negativos, la aceleración de la gravedad es descendente, por eso el signo -.
Trayectoria en caída libre
La trayectoria de caída libre es la distancia recorrida en ángulo determinado sea vertical u horizontal.
Caída libre totalmente vertical
El movimiento del cuerpo en caída libre es vertical con velocidad creciente (aproximadamente movimiento uniformemente acelerado con aceleración g) (aproximadamente porque la aceleración aumenta cuando el objeto disminuye en altura, en la mayoría de los casos la variación es despreciable). La ecuación de movimiento se puede escribir en términos la altura y:
(1)
Donde:
 , son la aceleración y la velocidad verticales.
, son la aceleración y la velocidad verticales. , es la fuerza de rozamiento fluidodinámica (que es creciente con la velocidad).
, es la fuerza de rozamiento fluidodinámica (que es creciente con la velocidad).
- Si se desprecia en una primera aproximación la fuerza de rozamiento, cosa que puede hacerse para caídas desde pequeñas alturas de cuerpos relativamente compactos, en las que se alcanzan pequeñas velocidades la solución de la ecuación diferencial () para las velocidades y la altura vienen dada por:
Donde v0 es la velocidad inicial, para una caída desde el reposo v0 = 0 y h0 es la altura inicial de caída.
- Para grandes alturas u objetos de gran superficie (una pluma, un paracaídas) es necesario tener en cuenta la fricción del aire que suele ser modelizada como una fuerza proporcional a la velocidad, siendo la constante de proporcionalidad el llamado rozamiento aerodinámico kw:
(2)
En este caso la variación con el tiempo de la velocidad y el espacio recorrido vienen dados por la solución de la ecuación diferencial ():
Nótese que en este caso existe una velocidad límite dada por el rozamiento aerodinámico y la masa del cuerpo que cae:
- Un análisis más cuidado de la fricción de un fluido revela que a grandes velocidades el flujo alrededor de un objeto no puede considerarse laminar, sino turbulento y se producen remolinos alrededor del objeto que cae de tal manera que la fuerza de fricción se vuelve proporcional al cuadrado de la velocidad:
(3)
Donde:
 , es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo.
, es el coeficiente aerodinámico de resistencia al avance, que sólo depende de la forma del cuerpo. , es el área transversal a la dirección del movimiento.
, es el área transversal a la dirección del movimiento.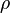 , es la densidad del fluido.
, es la densidad del fluido.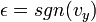 , es el signo de la velocidad.
, es el signo de la velocidad.
La velocidad límite puede calcularse fácilmente poniendo igual a cero la aceleración en la ecuación ():
La solución analítica de la ecuación diferencial () depende del signo relativo de la fuerza de rozamiento y el peso por lo que la solución analítica es diferente para un cuerpo que sube hacia arriba o para uno que cae hacia abajo. La solución de velocidades para ambos casos es:
0\\ v_y(t)= \sqrt{\cfrac{g}{\alpha}} \tanh\left(-t\sqrt{{\alpha}{g}} -\mbox{arctanh}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right) \right) & v_y(t) \le 0 \end{cases}" src="http://upload.wikimedia.org/math/7/3/7/737332b20f738aeba03bd69c33238a24.png">
Donde:  .
.
Si se integran las ecuaciones anteriores para el caso de caída libre desde una altura h0 y velocidad inicial nula y para el caso de lanzamiento vertical desde una altura nula con una velocidad inicial v0 se obtienen los siguientes resultados para la altura del cuerpo:
Caída libre (v0 = 0 y y(0) = h0):
El tiempo transcurrido en la caída desde la altura y = h0 hasta la altura y = 0 puede obtenerse al reordenar la ecuación anterior:
Lanzamiento vertical (v0 = v0 y y(0) = 0):
Si la altura h0 es aquella en que la velocidad vertical se hace cero, entonces el tiempo transcurrido desde el lanzamiento hasta el instante en que se alcanza la altura h0 puede calcularse como:
Se puede demostrar que el tiempo que tarda un cuerpo en caer desde una altura h0 hasta el suelo a través del aire es mayor que el que tarda el mismo cuerpo en alcanzar la alura máxima de h0 si es lanzado desde el suelo. Para ello basta con probar la desigualdad siguiente:
\mbox{arccos}\left(e^{-{\alpha}h_0}\right)" src="http://upload.wikimedia.org/math/f/9/3/f939f919ae4ae128ceb15f1753bedef6.png">
0" src="http://upload.wikimedia.org/math/a/1/4/a147bbbf568a0f108748277fa85db05f.png">
sabiendo que  y que
y que ![\mbox{arccos}\left(e^{-{\alpha}h_0}\right)\in\left[0,\cfrac{\pi}{2}\right]](http://upload.wikimedia.org/math/2/a/8/2a8f254b20cdbb409d09efc8c1990a48.png)
Caída libre parabólica y casi-parabólica [editar]
Cuando un cuerpo cae en caída libre pero no parte del reposo porque tiene una velocidad no nula, entonces la trayectoria de caída no es una recta sino una curva aproximadamente parabólica. La ecuación de la trayectoria en coordenadas cartesianas, donde x va a ser la distancia recorrida horizontalmente y y la altura sobre el nivel del suelo viene dada simplemente por:
(4)
Donde la expresión de la velocidad vertical debe reescribirse en función de la coordanada x teniendo en cuenta que t = x/vx. Pueden distinguirse los siguientes casos:
- Para un cuerpo en caída libre sin rozamiento la curva trayectoria es exactamente una parábola dada por:
- Cuando se incluye el rozamiento aerodinámico la curva no es exactamente una parábola. Por ejemplo para una fuerza de rozamiento proporcional a la velocidad como en la () la trayectoria resulta ser:
Para una fuerza de rozamiento proporcional al cuadrado de la velocidad la integración de las ecuaciones del movimiento es más compleja, presuponiendo fuerzas de rozamiento independientes en dirección horizontal y vertical proporcionales al cuadrado del valor de la componente:
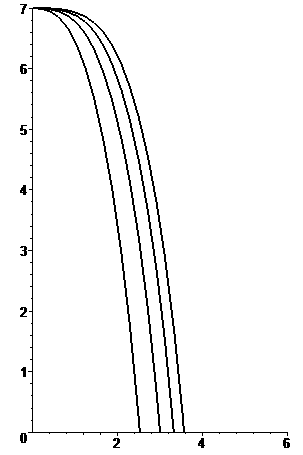
La trayectoria viene dada por:
Las figuras adjuntas muestran la forma de las trayectorias para cinco valores diferentes del parámetro β para una misma altura de caída (medida en unidades de longitud δ).
Caida Libre de los Cuerpos
Para la caida libre hasta el siglo XVI se aceptaba las
enseñanzas del gran sabio de la Antigüedad,
Aristóteles, que sostenían que los objetos pesados
caen más rápido que los ligeros.
Caida Libre, Principio: sabemos que si soltamos un
martillo y una pluma o una hoja de papel desde una
misma altura, el martillo alcanzará primero el piso.
Si arrugamos el papel dándole forma de bola se
observa que ambos objetos llegarán al piso casi al
mismo tiempo.
Fue el célebre italiano Galileo Galilei quien rebatió la
concepción de Aristóteles al afirmar que, en ausencia
de resistencia de aire, todos los objetos caen con una
misma aceleración uniforme. Pero Galileo no disponía
de medios para crear un vacío succionando el aire.
Las primeras máquinas neumáticas capaces de hacer
vacío se inventaron después, hacia el año 1650.
Tampoco disponía de relojes suficientemente exactos
o de cámaras fotográficas de alta velocidad. Sin
embargo, ingeniosamente probó su hipótesis usando
planos inclinados, con lo que conseguía un movimiento
más lento, el que podía medir con los rudimentarios
relojes de su época. Al incrementar de manera gradual
la pendiente del plano dedujo conclusiones acerca de
objetos que caían libre mente.
En el año 1971 un astronauta realizó en la Luna, donde
no existe atmósfera, el experimento de soltar desde
una misma altura y simultáneamente un martillo y una
pluma. Ambos objetos hicieron contacto con la
superficie lunar al mismo tiempo.
Cuando se emplea el término objeto en caída libre se incluye
tanto el soltar como el lanzar hacia arriba o hacia abajo el
objeto. Cualquier objeto que cae libremente tiene una
aceleración dirigida hacia abajo, independientemente del
movimiento inicial del objeto. La magnitud de esta aceleración
de caída libre se denota con el símbolo g, cuyo valor varía
ligeramente con la altura y con la latitud. En la cercanía de la
superficie de la Tierra el valor de g es aproximadamente 9,8 m/s2.
Ahora, la causa de esta aceleración fue encontrada por Newton,
quien estableció en su ley de Gravitación Universal que las masas
se atraen en proporción directa al producto de sus masas e
inversamente a su separación al cuadrado. Es la masa de la Tierra
la que origina esta aceleración de 9,8 m/s2 en su superficie.
La caída libre es un ejemplo común de movimiento uniforme-
mente acelerado, con una aceleración a = -9,8 m/s2. El signo
menos indica que la aceleración está dirigida en sentido contrario
al eje en dirección vertical (eje apuntando verticalmente hacia
arriba). Si se escoge el eje vertical en dirección hacia la Tierra,
la aceleración se toma como a = +9,8 m/s2.
Las ecuaciones cinemáticas para el movimiento en una línea
recta bajo la aceleración de gravedad son las mismas que para cualquier movimiento con aceleración constante:

El subíndice i denota cantidades iniciales, g la aceleración de
gravedad y t, el tiempo.
LAS CAJAS DE EINSTEIN
Existe una relación muy profunda entre sistemas de referencia no inercial y sistemas de referencia sometidos a fuerzas gravitacionales, relación que se puede entender con un ejemplo dado por el mismo Einstein.
Supongamos que nos encontramos encerrados en una caja colocada sobre la superficie terrestre. En su interior, sentimos la fuerza gravitacional de la Tierra que nos atrae al suelo, al igual que todos los cuerpos que se encuentran a nuestro alrededor. Al soltar una piedra, ésta cae al suelo aumentando continuamente su velocidad, es decir acelerándose a razón de 9.81 metros por segundo cada segundo, lo que equivale, por definición, a una aceleración de 1 g. Por supuesto, en el interior de la caja la fuerza que actúa sobre un cuerpo es proporcional a su masa gravitacional.

Ahora, consideramos el caso de una caja situada en el espacio, lejos de la influencia gravitacional de cualquier planeta o estrella. Si esa caja está en reposo, todo lo que se encuentra en su interior flota ingrávidamente. Pero si la caja se acelera, aumentado su velocidad a razón de 9.81. metros por segundo cada segundo (1 g), los objetos en su interior se quedan rezagados y se pegan al suelo; más aún, un cuerpo que se suelte dentro de ella se dirigirá al suelo con una aceleración de l g. Evidentemente, la caja acelerada es un sistema de referencia no inercial, y las fuerzas, que aparecen en su interior son fuerzas inerciales que dependen de la masa inercial de los cuerpos sobre los que actúan.
Y ahora la pregunta fundamental: ¿pueden los ocupantes de una caja determinar por medio de experimentos físicos si se encuentran en reposo sobre la superficie de la Tierra o se encuentran en el espacio, en movimiento acelerado? La respuesta es no, porque el principio de equivalencia no permite distinguir, dentro de la caja, entre una fuerza gravitacional y una inercial.
Podemos imaginarnos otra posible situación. Esta vez la caja es un elevador que se encuentra en un edificio terrestre, pero su cable se rompe y cae libremente. Sus ocupantes caen junto con la caja (Figura 24) y, mientras dura la caída, no sienten, ninguna fuerza gravitacional, exactamente como si estuvieran en el espacio extraterrestre.
Otra situación, que se ha vuelto familiar en los últimos años, es la de los cosmonautas que vemos flotar ingrávidos dentro de sus vehículos colocados en órbita alrededor de la Tierra. Si no perciben ninguna fuerza gravitacional no es porque estén tan alejados de la Tierra que no resientan su atracción, es porque él vehículo espacial y sus tripulantes se encuentran en caída libre. Esto puede no coincidir con la idea, común de Luna caída; pero hay que recordar que, estrictamente hablando, un cuerpo se encuentra en caída libre si se mueve únicamente bajo el influjo de una fuerza gravitacional sin otro tipo de restricción. Un satélite terrestre efectivamente está en caída libre, pero nunca choca con la Tierra por la curvatura de ésta, como se puede ver en la figura 26. En resumen, un vehículo espacial en órbita, con sus motores apagados y sin fricción del aire por encontrarse fuera de la atmósfera, es un ejemplo perfecto de un sistema inercial: sus ocupantes no pueden decidir, sin mirar por las escotillas, si están en órbita alrededor de la Tierra o en reposo lejos de todo cuerpo celeste.

Así, un sistema de referencia inercial es equivalente a un sistema de referencia en caída libre, y del mismo modo un sistema no inercial es equivalente a un sistema de referencia sometido a la fuerza gravitacional. En consecuencia, se puede extender el principio de relatividad a sistemas no inerciales si se toma en cuenta a la gravitación. Pero Einstein fue más allá de esta simple comprobación.

Un satélite en órbita es un caso extremo de proyectil de caída libre.
Regresemos al ejemplo de la caja en caída libre, pero esta vez supongamos que la caja es lo suficientemente grande para hacer el siguiente experimento: colóquense dos canicas en cada extremo del compartimiento, como se indica en la figura 27. Como las canicas se hallan también en caída libre, permanecen fijas, flotando, para los ocupantes de la caja. Sin embargo, las trayectorias de ambas no son exactamente rectas paralelas, sino rectas que convergen al centro de la Tierra. En consecuencia, vistas desde la caja, las dos canicas no están estrictamente fijas, sino que parecen acercarse lentamente una a otra. Este efecto casi imperceptible no ocurriría si la caja estuviera en el espacio extraterrestre, lejos de todo influjo gravitacional, ya que las dos canicas permanecerían exactamente donde se colocan.

Manifestación de la fuerza gravitacional en una caja en caída libre suficientemente grande.
El experimento anterior implica que la equivalencia entre sistema inercial y sistema en caída libre debe formularse con más precisión: Los dos sistemas son equivalentes en una región pequeña del espacio, pero pueden distinguirse uno del otro si se realizan experimentos físicos sobre distancias suficientemente grandes.
Esta comprobación condujo a Einstein a relacionar la gravitación con las propiedades geométricas de una superficie. Por ejemplo, sabemos que la Tierra es redonda, pero su curvatura no se manifiesta en una región pequeña. A escala humana, nuestro planeta parece plano y es sólo sobre distancias de varios cientos de kilómetros que los efectos de la curvatura se vuelven apreciables. Si se trazan dos rectas paralelas sobre la superficie terrestre, estas rectas permanecen paralelas inicialmente manteniéndose constante la distancia entre ellas; pero si las rectas se prolongan cientos de kilómetros empezarán a converger debido a la curvatura de la Tierra, y acabaran por unirse en algún punto (Figura 28). Las rectas trazadas sobre la superficie de la Tierra son más bien segmentos de círculo; es sólo a escalas pequeñas que parecen rectas. El concepto de recta pierde su sentido sobre una superficie curva y es más preciso referirse a curvas de longitud mínima: sobre una superficie plana, la recta es la curva de mínima longitud entre dos puntos dados, pero sobre la superficie de una esfera la curva más corta entre dos puntos es un segmento de círculo (Figura 29).

Dos "paralelas" terminan uniéndose sobre una superficie curva.
Ahora bien, las dos "paralelas" trazadas sobre la superficie de la Tierra, y que terminan por unirse debido a la curvatura de ésta, recuerdan las trayectorias de las dos canicas en el elevador que cae. En el primer caso, se tiene un efecto debido a la curvatura de una superficie, mientras que en el segundo caso se manifiesta una fuerza gravitacional. El primer efecto es geométrico y el segundo gravitacional. Una superficie curva parece plana en una región suficientemente pequeña, y del mismo modo una fuerza gravitacional no es detectable en un vehículo de dimensiones reducidas y en caída libre.

Las geodésicas son las curvas de menor longitud sobre una superficie curva.
Todas estas analogías condujeron a Einstein a la conclusión de que la fuerza gravitacional puede interpretarse como un efecto geométrico. Sólo que, a diferencia de la superficie terrestre, en la teoría de Einstein el espacio-tiempo es curvo y la gravitación es la manifestación de su curvatura.
MARCO TEORICO
En cinemática, la caída libre es un movimiento de un cuerpo dónde solamente influye la gravedad. En este movimiento se desprecia el rozamiento del cuerpo con el aire, es decir, se estudia en el vacío. El movimiento de la caída libre es un movimiento uniformemente acelerado. La aceleración instantánea es independiente de la masa del cuerpo, es decir, si dejamos caer un coche y una pulga, ambos cuerpo tendrán la misma aceleración, que coincide con la aceleración de la gravedad (g). Esto lo podemos demostrar del siguiente modo:
Sabemos por la segunda ley de Newton que la fuerza es igual al producto entre la masa del cuerpo y la aceleración.

La única fuerza que influye en la caída libre (recordamos que se desprecia el rozamiento con el aire) es el peso, que es igual al producto entre la masa del cuerpo y la constante gravitatoria g.

Despejamos de la primera ecuación la aceleración.

Sustituimos la fuerza.

Por lo tanto nos queda que la aceleración del cuerpo siempre coincide con la constante gravitatoria

Otra forma de demostrar que la aceleración de los cuerpos en caída libre en el vacío tiene que ser la misma sin importar el peso de los objetos, es mediante un simple desarrollo lógico:
Supongamos dos cuerpos, el primero del doble de peso que el segundo. Ahora, interpretemos al primer objeto como dos de los segundos objetos unidos de alguna forma, entonces la aceleración del objeto más pesado debería ser la misma que la de cada uno de los dos objetos más livianos, puesto que si así no fuera entonces un cuerpo debería caer a diferentes velocidades dependiendo de si lo vemos como un solo objeto o como sus partes unidas.



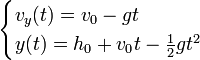





![y(t)=h_0-\cfrac{1}{{\alpha}}\ln\left[\cosh\left(-t\sqrt{{\alpha}{g}}\right) \right]](http://upload.wikimedia.org/math/6/4/4/64407f2d5c666902f084e7350c123773.png)

![y(t)=\cfrac{1}{{\alpha}}\ln\left[\cfrac{\cos\left[-t\sqrt{{\alpha}{g}}+\arctan\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]}{\cos\left[\mbox{arctan}\left(v_0\sqrt{\cfrac{\alpha}{g}}\right)\right]} \right]](http://upload.wikimedia.org/math/1/6/2/162a803c65007695a5634885c3c8cce0.png)



![y(x) = h_0 - \delta \left[\frac{x}{\beta\delta}-\ln \left(1-\frac{x}{\beta\delta} \right) \right] \qquad \begin{cases} \delta = gm^2/k_w^2\\ \beta = V_xk_w/mg\end{cases}](http://upload.wikimedia.org/math/2/4/9/2499cfce560492266eba090a5e021837.png)

![y(x) = h_0 - \delta \ln \left[\cosh \left( \frac{e^{x/\delta}-1}{\beta}\right) \right] \qquad \begin{cases} \delta = 1/C_w\\ \beta = \sqrt{g/(C_wV_x^2)} \end{cases}](http://upload.wikimedia.org/math/3/b/f/3bf3fe9845c590f97bd6f85495e3efd4.png)

0 comentarios